An agent-based model of community joining

Jeremy Foote
Northwestern University

Benjamin Mako Hill
University of Washington

Nate TeBlunthuis
University of Washington

How do we decide which groups to join?
Groups size distributions vary
Universities look like this: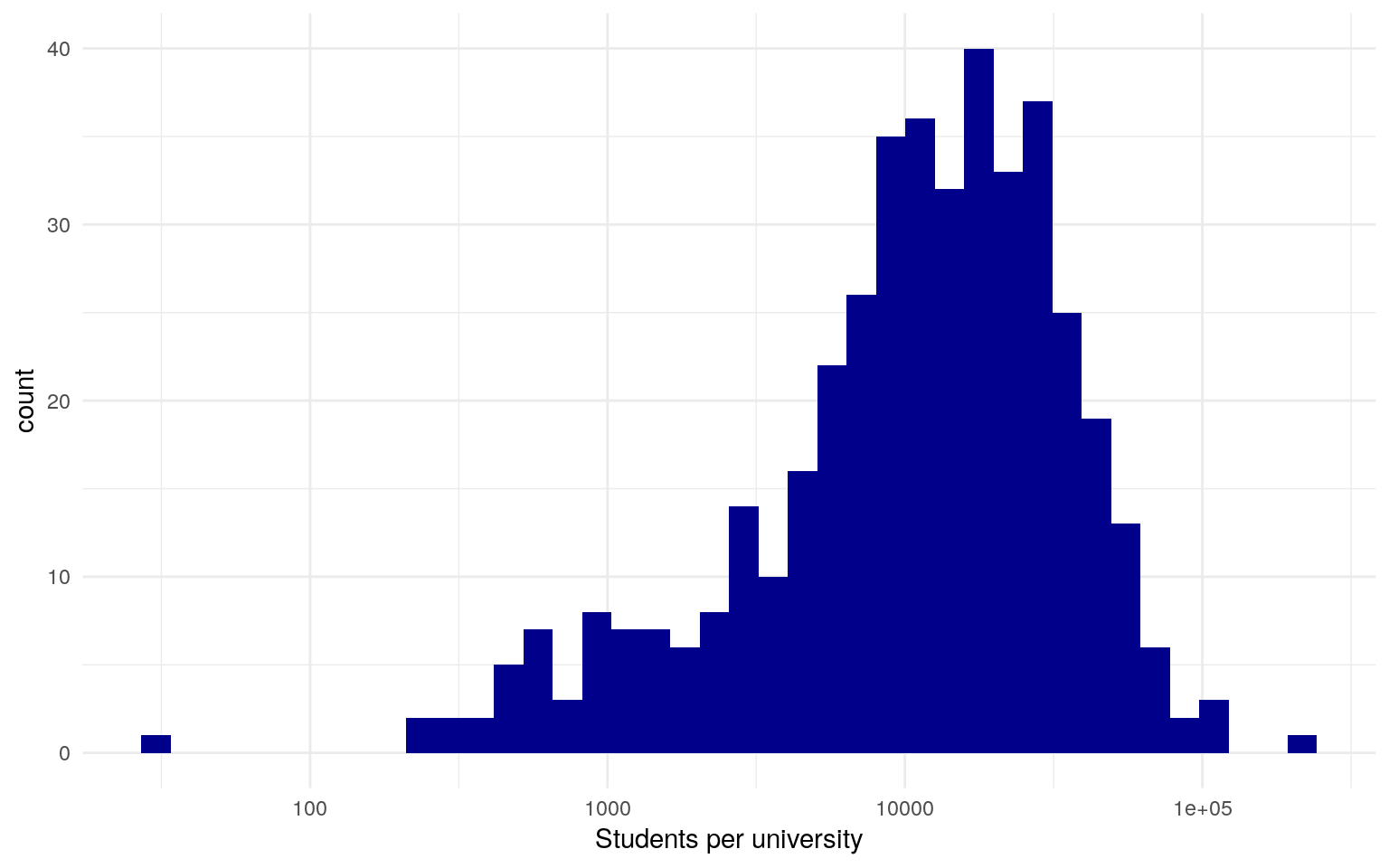
Data from Wikidata
Online groups
While reddit looks like this:
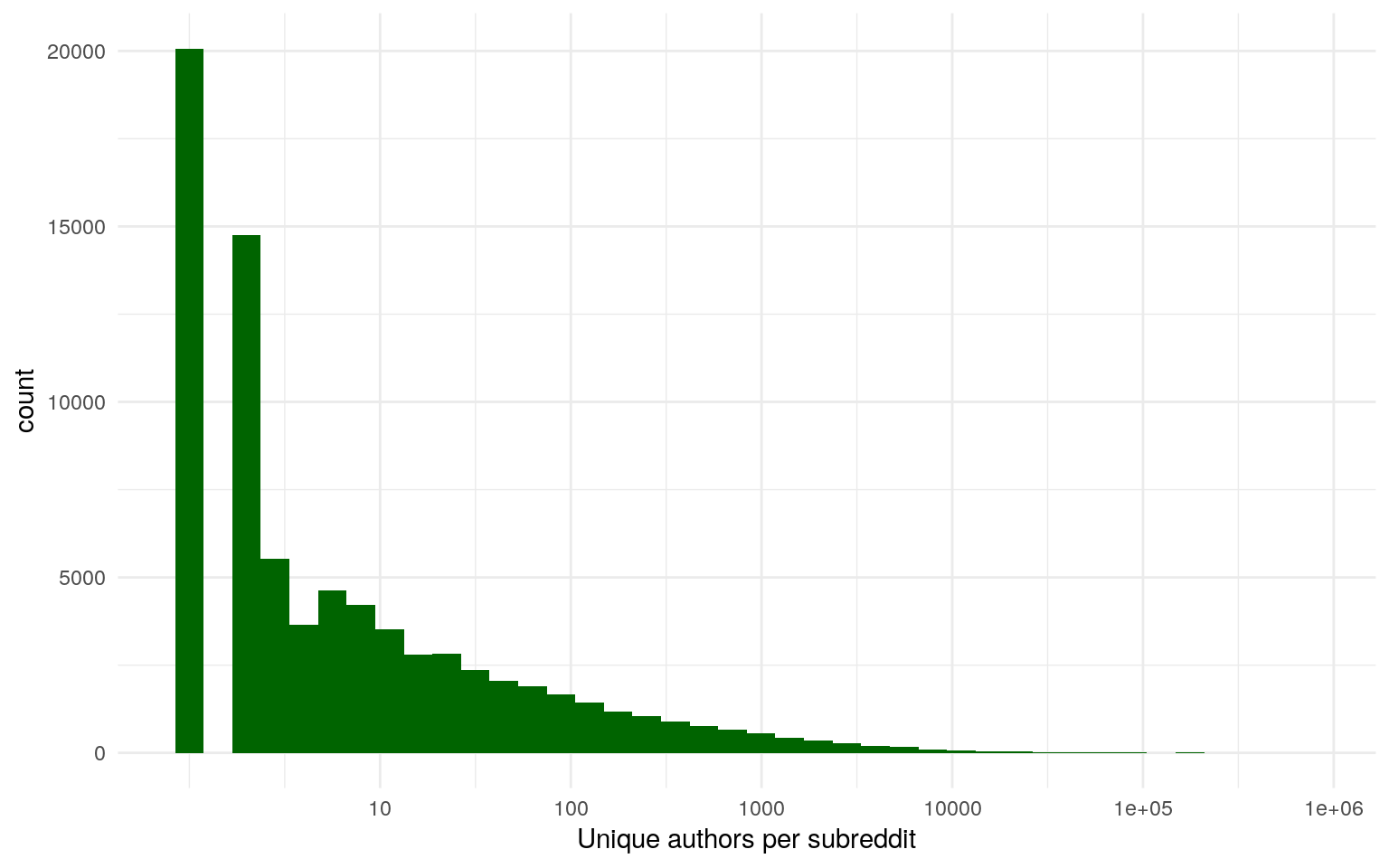
Data from Stuck_in_the_Matrix on BigQuery
Why?
Preferential Attachment
- One model proposed as source of long-tail distributions is preferential attachment (Barabási, 1999)
- People probabilistically join groups based on their relative size
One small problem
- It’s not realistic
- Observed distributions often aren’t power-law (Broido and Clauset, 2018)
- People don’t make decisions in this way
A better model
Expected value of joining
- Resnick et al. (2011)
- People estimate the benefits of joining
- Participation benefits (information, friendship)
- Based on estimate of future growth
- Early adopter benefits (influence)
- Estimate the costs (new technology, learning new norms, etc.)
- Join if benefits exceed costs
A few problems
- Only applies to single decision
- Doesn’t explain how people estimate future growth
- Not derived from empirical data
Is it reasonable?
Our agent-based model
- Basic structure
- Start with \(N\) potential contributors and \(X\) empty communities
- Every “month”:
- \(X\) new communities are created
- \(n\) users are chosen at random
- Each user is presented with a “choice set” of \(x\) communities
- Choice sets are randomly chosen, weighted by community size
- The user estimates the future size and joins the community with the greatest expected utility
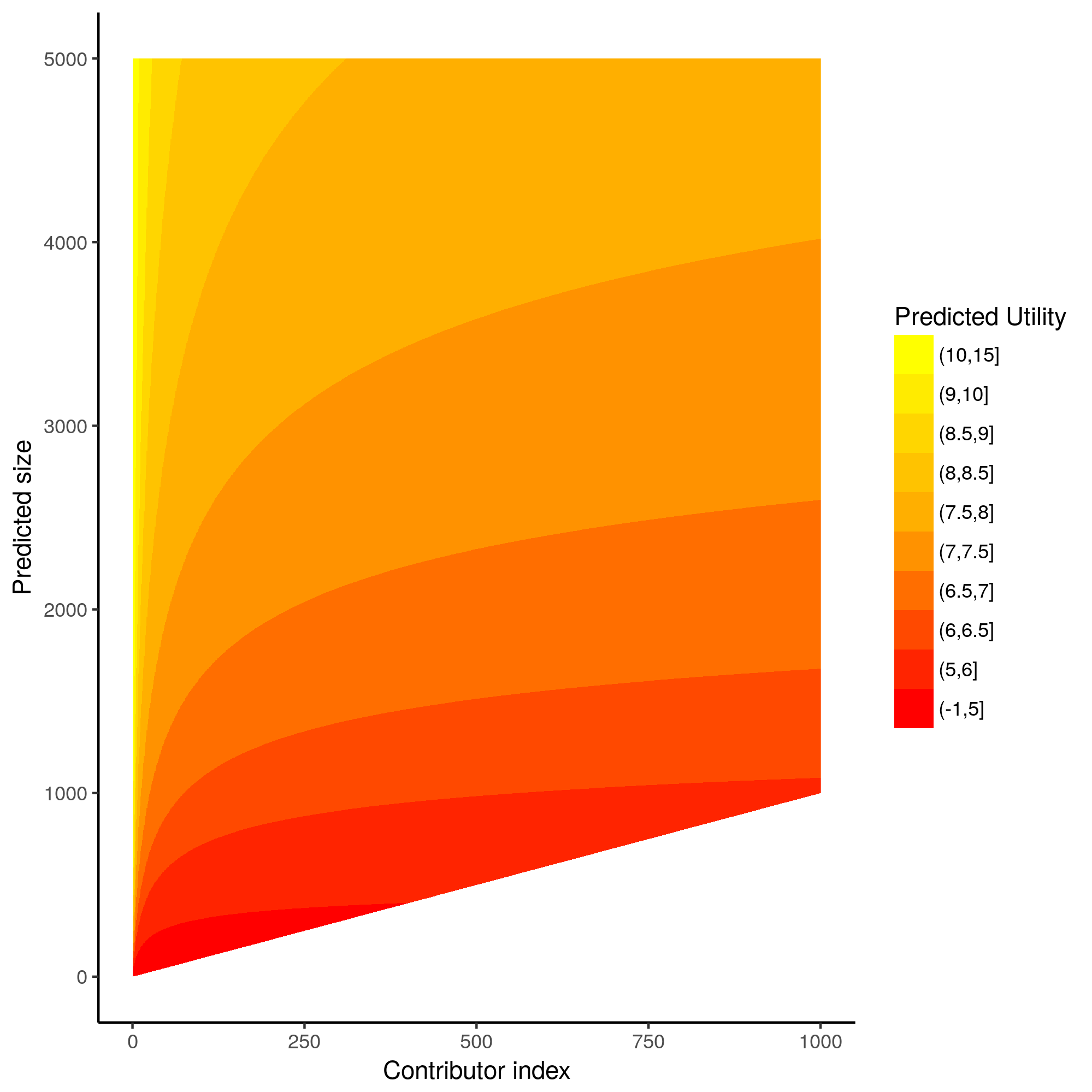
Utility
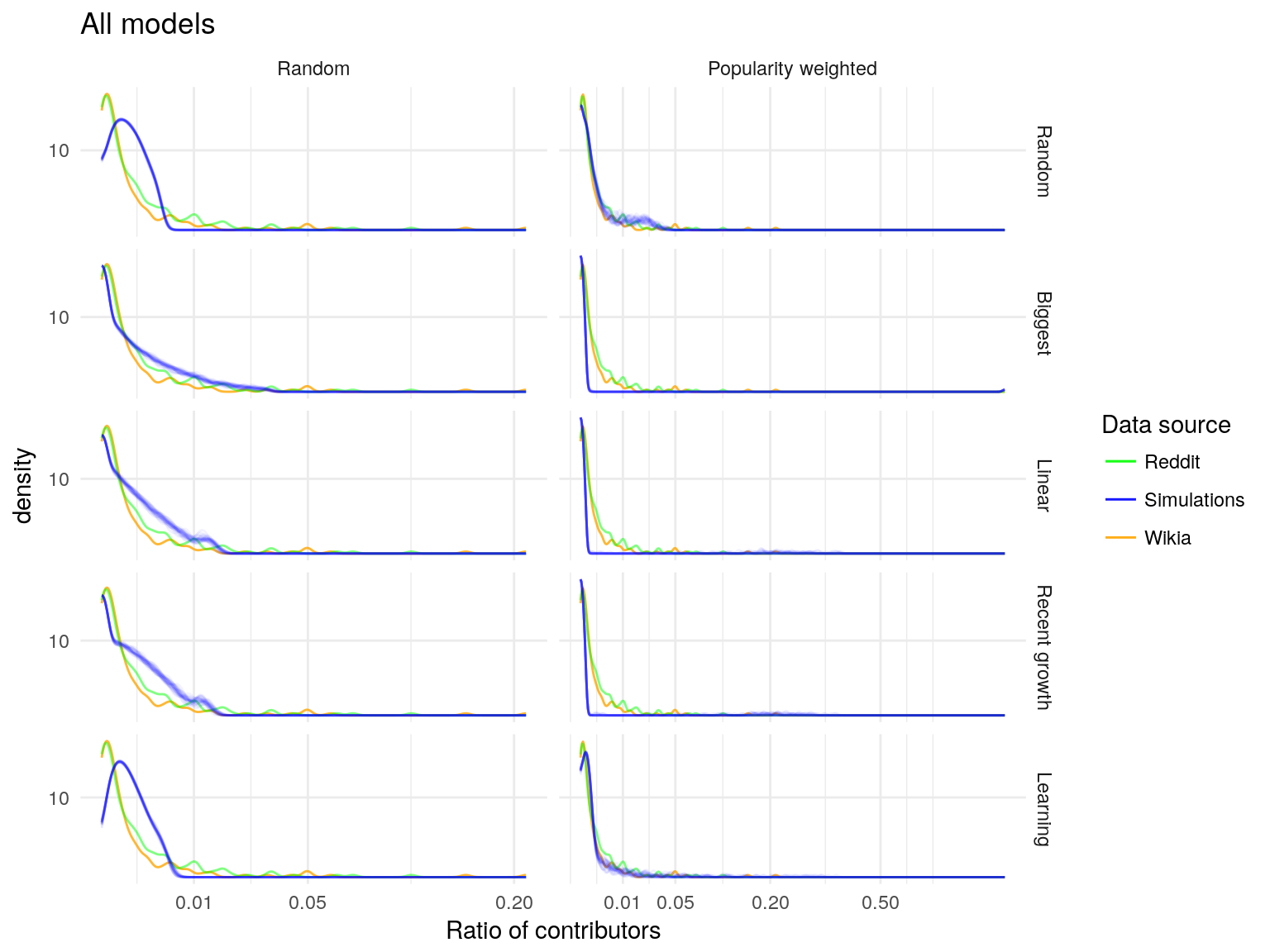
Decision algorithms
- Random
- Biggest
- Linear growth
- Recent growth
- Learning model
Learning model
- Agents fit a regression model on previously joined communities
- They then predict the growth of their current choice set
Results
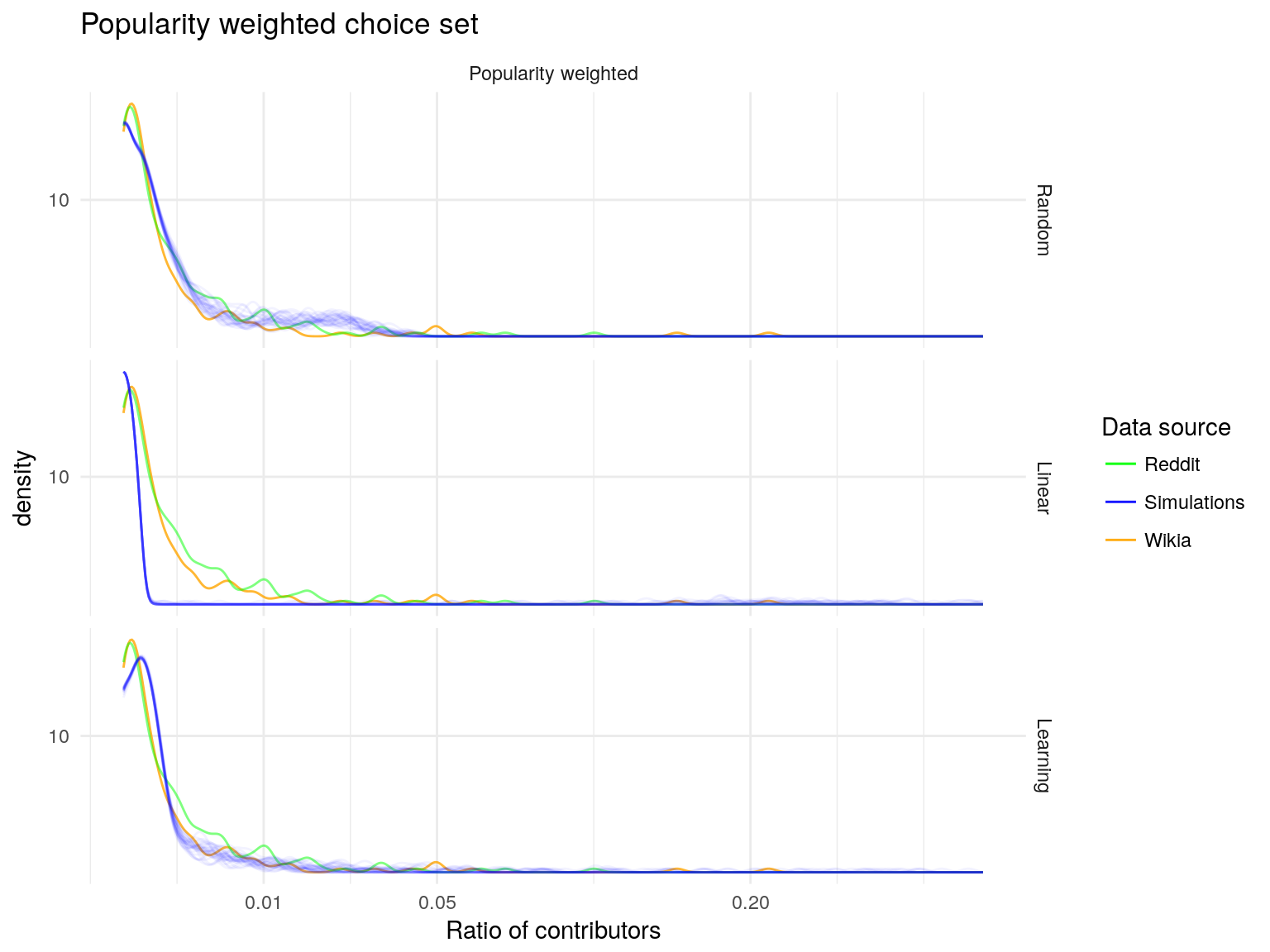
Empirical distributions
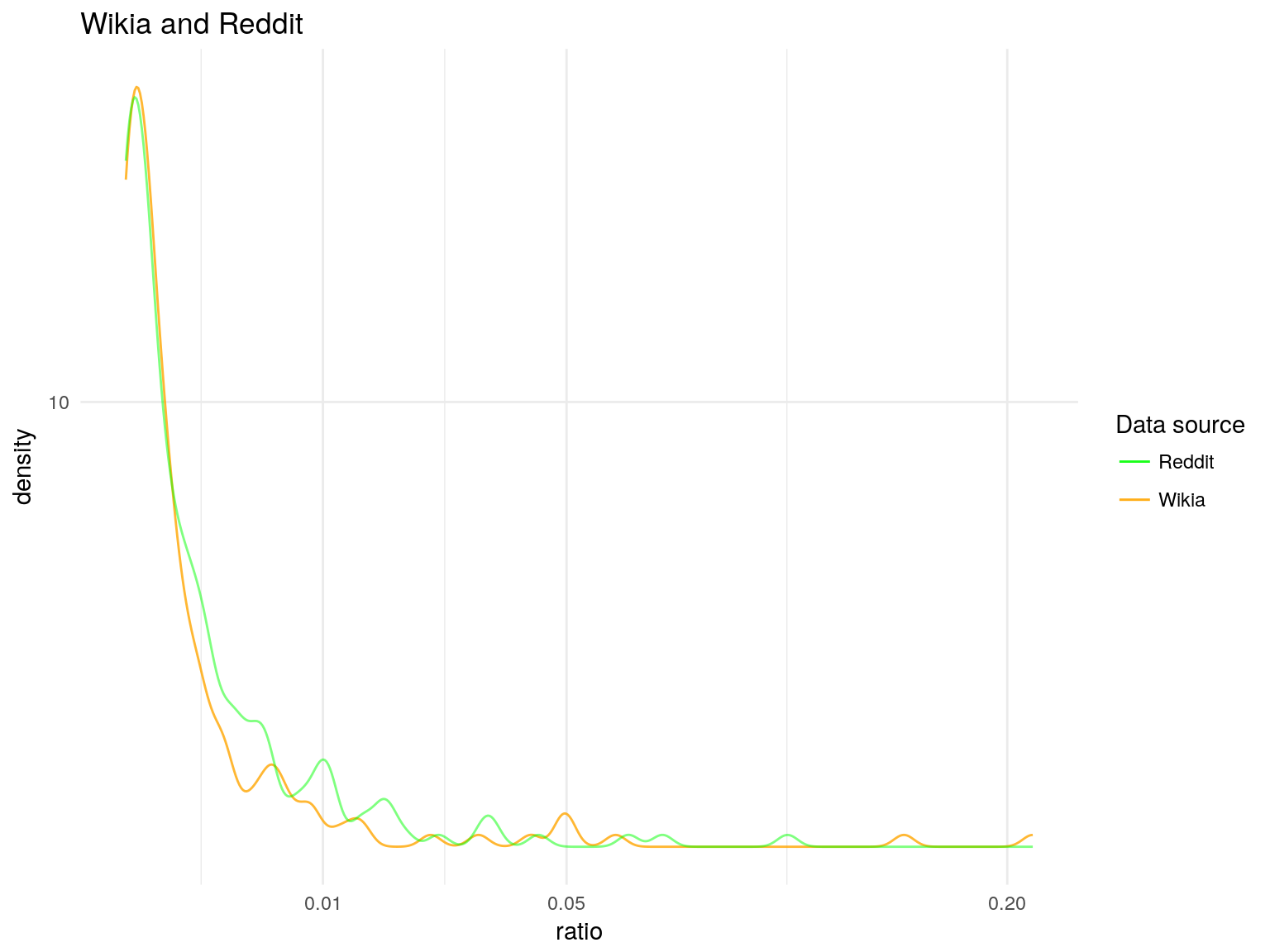
Simulated distributions
Limitations
Agent-based modeling
- Better for disproving than proving
- Other models could match just as well
- Choices about where and how to simplify
Future work
- Surveys and experiments
- Do past experiences influence decisions?
- What do actual “choice sets” look like?
- Modeling interests explicitly
- Explaining longitudinal patterns of participation
Conclusion
A more realistic model
- We don’t need preferential attachment*
- A Resnick et al. model can produce realistic distributions
- But it’s very sensitive to how people make estimates
- Only learning models produced realistic outcomes
- Likely due to heterogeneity in expectations
The End
Thanks!

Jeremy Foote
@jdfoote

Benjamin Mako Hill
@makoshark

Nate TeBlunthuis
@groceryheist

Appendix
Utility
- Participation benefits (PB)
- \(PB = log(S + 1)\)
- Early adopter benefits (EA)
- \(EA = log(S + 1)/log(i + 1)\)
- Cost = \(X\)
- \(U = PB + EA - C\)
Learning model:
\[\begin{align} log(growth) &=\beta_0 + \beta_1 \times S_j + \beta_2 \times A_j \\\ &+ \beta_3 \times (A_c - A_j) + \beta_4 \times S_c \end{align}\]- \(S_c\) = current size, \(A_j\) = age when joined
- Predicted size after 6 months
All models
–> –> –> –>
–> –> –> –> –> –> –> –>
–>