My wife and I recently had our fourth(!) child. He is really wonderful and having an infant in the house has been magical and fantastic.

However, I’ve noticed that even though the baby has been well-behaved and even sleeps pretty well, our home life has felt more stressful and chaotic. At first, I chalked it up to the effects of getting less sleep and the start of a new school year. Kids don’t always deal well with change.

While I think that’s a reasonable explanation, I realized that there’s also a mathematical explanation. Being a parent of young kids has lots and lots of great moments, but it also has its stresses. One of the most stressful is when kids have a meltdown. Dealing with a child who can’t control themselves or their emotions takes the full attention of a parent and takes a lot of emotional and mental energy. When two children are melting down at the same time, even with two parents around, it’s incredibly stressful. When one kid is having problems, the other parent can pick up some of the slack (helping the other kids, making dinner, etc.). When both parents are occupied, nothing else gets done.

I realized that as the number of kids goes up, the probability of two or more having a meltdown goes up very quickly (at first). If we assume that meltdowns are independent¹ and children have a constant probability of meltdown, then whether any given child is melting down can be treated like a coin flip, and the number of meltdowns in a given time period can be modeled as a binomial distribution. A binomial distribution is the probability of successes in a given number of trials (e.g., the number of heads in 10 coin flips). Formally, the chance of having more than x simultaneous meltdowns in a given time period is equal to

where n is the number of children, and p is each child’s probability of melting down.

So, if we look at the chance of having at least 2 simultaneous meltdowns, and assume that each child has an individual meltdown probability of .1 in a given half hour:

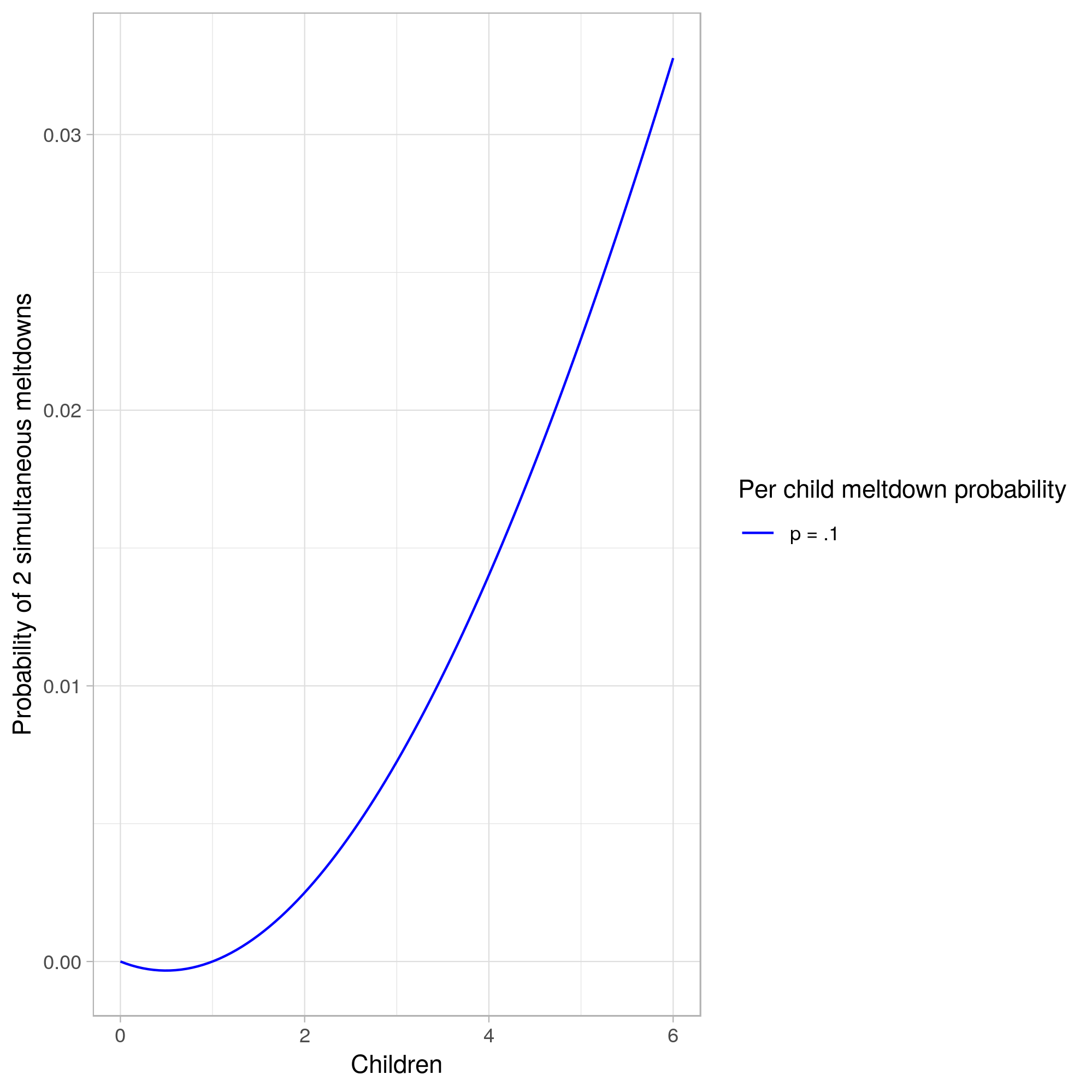
At those meltdown rates, with 3 children, we had a 2.8% chance of experiencing a two-or-more-person meltdown at any given time. However, with our fourth child, we’ve nearly doubled that likelihood, to 5.2%.

Things look even worse if we consider it at the level of a day. In the four hours after school and before bed, with three kids we had a 20% chance of seeing a two-person meltdown each day, but with four we’ve moved to a 35% chance.

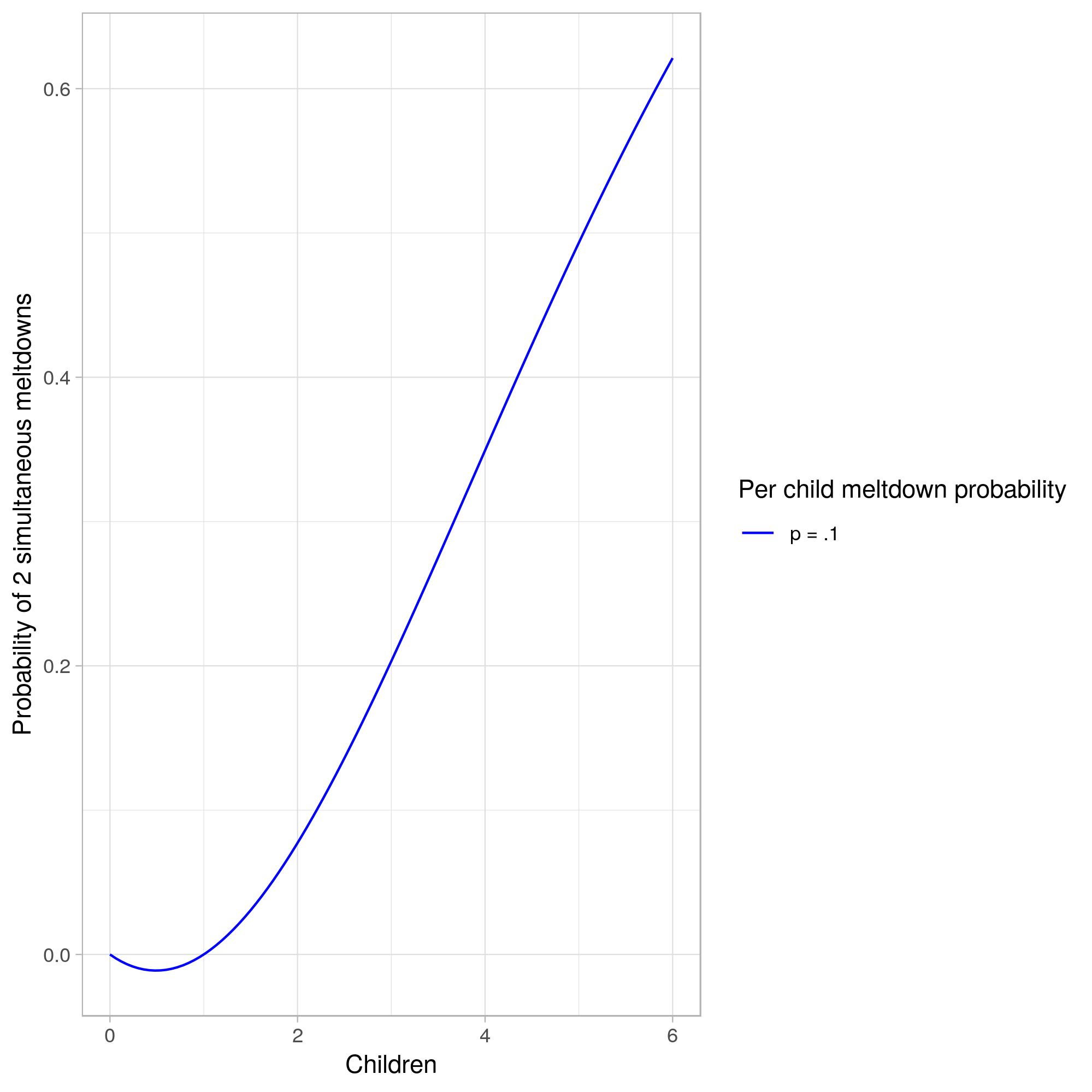
In reality, meltdowns are correlated, and one child’s meltdown often causes another’s, exacerbating the problem!

The lesson of this post is not to avoid having lots of kids! There are lots of great things about kids that also scale super-linearly. The lesson for me is that probabilistic thinking does not come naturally but can be a powerful tool in understanding the world.

1: Of course, meltdowns are likely to be correlated, as one child’s meltdown can directly cause another’s!